Difference between revisions of "Advection and Groundwater Flow"
m (1 revision imported) |
m (1 revision imported) |
(No difference)
| |
Revision as of 19:22, 2 May 2018
Advection is the movement of groundwater through the subsurface due to pressure and gravitational energy. The combined processes of advection, dispersion, diffusion, sorption, and degradation control how long a contaminant plume will grow, remain stable, or shrink, as well as how easy or difficult it will be to remediate. The combined effects of these processes are represented in solute transport models with the advection-dispersion-reaction equation.
Related Article(s):
CONTRIBUTOR(S): Dr. Charles Newell, P.E.
Key Resource(s):
Groundwater Flow
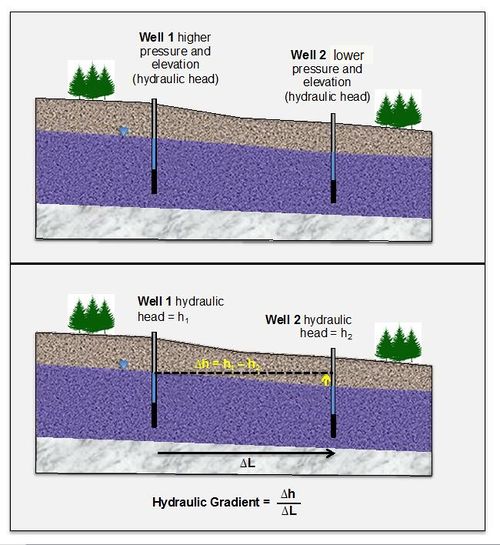
Groundwater will flow from areas of high hydraulic head (pressure and gravitational energy) to areas of lower hydraulic head (Fig. 1). The slope of the change in hydraulic head is known as the hydraulic gradient. If groundwater is flowing and contains dissolved contaminants it can transport the contaminants from areas with high hydraulic head to lower hydraulic head (or “downgradient”).
Darcy's Law
In unconsolidated geologic settings (gravel, sand, silt, and clay) and highly fractured systems, the rate of groundwater movement can be expressed using Darcy’s Law. This law is a fundamental mathematical relationship in the groundwater field and can be expressed this way:
- Where:
- Q = Flow per area (Volume groundwater flow per area per time, such as m3/yr)
- A = Cross sectional area perpendicular to groundwater flow (length2, such as m2)
- VD = “Darcy Velocity”; another way to describe groundwater flow as the flow per unit area (units of length per time, such as ft/yr)
- K = Hydraulic Conductivity (sometimes called “permeability”) (length per time)
- ΔH = Difference in hydraulic head between two lateral points (length)
- ΔL = Length between two lateral points (length)
- Where:
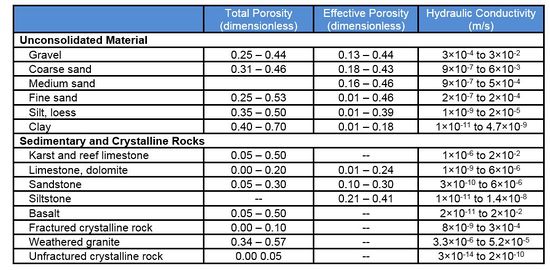
Hydraulic conductivity (Table 1 and Fig. 2) is a measure of how easy groundwater flows through a porous medium, or alternatively, how much energy it takes to force water through a porous medium. For example, fine sand (sand with small grains) means smaller pores and more frictional resistance and therefore lower hydraulic conductivity (Fig. 2) compared to coarse sand (sand with large grains), which has less resistance to flow.
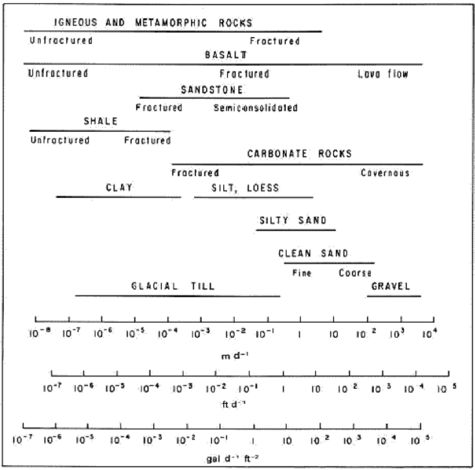
Darcy’s Law was first described by Henry Darcy (1856)[5] in a report regarding a water supply system he designed for the city of Dijon, France. He ran experiments and concluded that the amount of water flowing through a closed tube of sand (dark grey box in Figure 3) depends on (a) the change in the hydraulic head between the inlet and outlet of the tube, and (b) the hydraulic conductivity of the sand in the tube. Groundwater flows rapidly in the case of higher pressure (ΔH) and permeable materials such as gravel or coarse sand, but flows slowly when the pressure is lower and low-permeability material such as fine sand or silt.
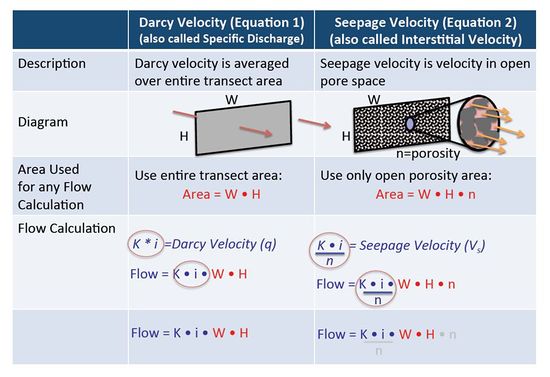
Since Darcy’s time, Darcy’s Law has been adapted to calculate the actual velocity that the groundwater is moving in units such as meters traveled per year. This quantity is called “interstitial velocity” or “seepage velocity” and is calculated by dividing the Darcy Velocity (flow per unit area) by the actual open pore area where groundwater is flowing, the “effective porosity” (Table 1):
- Where:
- VS = “interstitial velocity” or “seepage velocity” (units of length per time, such as m/sec)
- VD = “Darcy Velocity”; another way to describe groundwater flow as the flow per unit area (units of length per time)
- ne = Effective porosity (unitless)
- VS = “interstitial velocity” or “seepage velocity” (units of length per time, such as m/sec)
Effective porosity is smaller than total porosity. The difference is that total porosity includes some dead-end pores that do not support groundwater. Typically values for total and effective porosity are shown in Table 1.
Darcy Velocity and Seepage Velocity
In groundwater calculations, Darcy Velocity and Seepage Velocity are two different things used for different purposes. For any calculation where the actual flow rate in units of volume per time (such as liters per day or gallons per minute) is involved, then the original Darcy Equation should be used (calculate VD; Equation 1) without using effective porosity. When calculating solute travel time, then the seepage velocity calculation (VS; Equation 2) must be used and an estimate of effective porosity is required. Figure 4 illustrates the differences between Darcy Velocity and Seepage Velocity.
Mobile Porosity
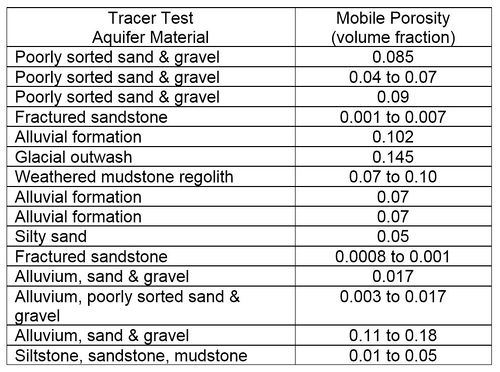
More recently, data from multiple short-term tracer tests conducted to design in situ remediation systems, have been analyzed to better understand contaminant migration in groundwater[6]. In these tests, the dissolved solutes were observed to migrate more rapidly through the aquifer than could be explained with typically reported values of ne. The interpretation is that the heterogeneity of unconsolidated formations results in a relatively small area of an aquifer cross section carrying most of the water, and so solutes migrate more rapidly than expected. Based on these results, the recommendation is that a quantity called “mobile porosity” should be used in place of ne in equation 2 for calculating solute transport velocities. Based on 15 different tracer tests, typical values of mobile porosity range from 0.02 to 0.10 (Table 2).
References
- ^ 1.0 1.1 Domenico, P.A. and Schwartz, F.W., 1998. Physical and chemical hydrogeology. John Wiley & Sons, 2nd Ed., 528 pgs. ISBN 978-0-471-59762-9.
- ^ McWhorter, D.B. and Sunada, D.K., 1977. Ground-water hydrology and hydraulics. Water Resources Publication, LLC. 304 pgs. ISBN 978-0-918334-18-3
- ^ Freeze, R.A. and Cherry, J.A., 1979. Groundwater. 604 pgs. ISBN 978-0133653120
- ^ Heath, R.C., 1983. Basic ground-water hydrology, U.S. Geological Survey Water-Supply Paper 2220, 86 pgs. Report pdf
- ^ Darcy, H., 1856. Les Fontaines Publiques de la Ville de Dijon, Dalmont, Paris. doi: 10.1029/2001WR000727
- ^ 6.0 6.1 Payne, F.C., Quinnan, J.A. and Potter, S.T., 2008. Remediation hydraulics. CRC Press. ISBN 978-1-4200-0684-1