Difference between revisions of "User:Jhurley/sandbox"
| Line 2: | Line 2: | ||
==Advection-Dispersion-Reaction Equation for Solute Transport== | ==Advection-Dispersion-Reaction Equation for Solute Transport== | ||
| − | The transport of dissolved solutes in groundwater is often modeled using the Advection-Dispersion-Reaction (ADR) equation. [[wikipedia:Advection|Advection]] refers to the bulk movement of solutes carried by flowing groundwater. [[wikipedia:Dispersion|Dispersion]] refers to the spreading of the contaminant plume from highly concentrated areas to less concentrated areas. Dispersion coefficients are calculated as the sum of [[wikipedia:Molecular diffusion | molecular diffusion]] mechanical dispersion, and macrodispersion. Reaction refers to changes in mass of the solute within the system resulting from biotic and abiotic processes. | + | The transport of dissolved solutes in groundwater is often modeled using the Advection-Dispersion-Reaction (ADR) equation. [[wikipedia:Advection|Advection]] refers to the bulk movement of solutes carried by flowing groundwater. [[wikipedia:Dispersion|Dispersion]] refers to the spreading of the contaminant plume from highly concentrated areas to less concentrated areas. Dispersion coefficients are calculated as the sum of [[wikipedia:Molecular diffusion | molecular diffusion]], mechanical dispersion, and macrodispersion. Reaction refers to changes in the mass of the solute within the system resulting from biotic and abiotic processes. |
<div style="float:right;margin:0 0 2em 2em;">__TOC__</div> | <div style="float:right;margin:0 0 2em 2em;">__TOC__</div> | ||
Revision as of 19:51, 4 September 2020
Advection-Dispersion-Reaction Equation for Solute Transport
The transport of dissolved solutes in groundwater is often modeled using the Advection-Dispersion-Reaction (ADR) equation. Advection refers to the bulk movement of solutes carried by flowing groundwater. Dispersion refers to the spreading of the contaminant plume from highly concentrated areas to less concentrated areas. Dispersion coefficients are calculated as the sum of molecular diffusion, mechanical dispersion, and macrodispersion. Reaction refers to changes in the mass of the solute within the system resulting from biotic and abiotic processes.
Related Article(s):
- Advection and Groundwater Flow
- Dispersion and Diffusion
- Sorption of Organic Contaminants
- Plume Response Modeling
CONTRIBUTOR(S):
Key Resource(s):
- Groundwater[1], Freeze and Cherry, 1979.
- Hydrogeologic Properties of Earth Materials and Principals of Groundwater Flow[2], Woessner and Poeter, 2020.
The ADR Equation
In many groundwater transport models, solute transport is described by the advection-dispersion-reaction equation. As shown below (Equation 3), the ADR equation describes the change in dissolved solute concentration (C) over time (t) where groundwater flow is oriented along the x direction.
- Where:
- R is the linear, equilibrium retardation factor (see Sorption of Organic Contaminants),
- Dx, Dy, and Dz are hydrodynamic dispersion coefficients in the x, y and z directions (L2/T),
- v is the advective transport or seepage velocity in the x direction (L/T), and
- λ is an effective first order decay rate due to combined biotic and abiotic processes (1/T).
The term on the left side of the equation is the rate of mass change per unit volume. On the right side are terms representing the solute flux due to dispersion in the x, y, and z directions, the advective flux in the x direction, and the first order decay due to biotic and abiotic processes. Dispersion coefficients (Dx,y,z) are commonly estimated using the following relationships:
- Where:
- Dm is the molecular diffusion coefficient (L2/T), and
- αL, αT, and αV are the longitudinal, transverse and vertical dispersivities (L).
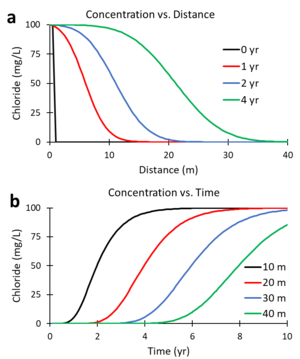
Figures 5a and 5b were generated using a numerical solution of the ADR equation for a non-reactive tracer (R = 1; λ = 0) with v = 5 m/yr and Dx = 10 m2/yr. Figure 5a shows the predicted change in concentration of the tracer, chloride, versus distance downgradient from the continuous contaminant source at different times (0, 1, 2, and 4 years). Figure 5b shows the change in concentration versus time (commonly referred to as the breakthrough curve or BTC) at different downgradient distances (10, 20, 30 and 40 m). At 2 years, the mid-point of the concentration versus distance curve (Figure 5a) is located 10 m downgradient (x = 5 m/yr * 2 yr). At 20 m downgradient, the mid-point of the concentration versus time curves (Figure 5b) occurs at 4 years (t = 20 m / 5 m/yr).
The dispersion coefficient in the ADR equation accounts for the combined effects of molecular diffusion and mechanical dispersion which cause the spreading of the contaminant plume from highly concentrated areas to less concentrated areas. Molecular diffusion is the result of the thermal motion of individual molecules which causes a flux of dissolved solutes from areas of higher concentration to areas of lower concentration. Mechanical dispersion (hydrodynamic dispersion) results from groundwater moving at rates that vary from the average linear velocity. Because the invading solute-containing water does not travel at the same velocity everywhere, mixing occurs along flow paths. Typical values of the mechanical dispersivity measured in laboratory column tests are on the order of 0.01 to 1 cm (Anderson and Cherry, 1979).
Matrix Diffusion is the process where dissolved contaminants are transported into low K zones by molecular diffusion, and then can diffuse back out of these low K zones once the contaminant source is removed. In some cases, matrix diffusion can maintain contaminant concentrations in more permeable zones above target cleanup goals for decades or even centuries after the primary sources have been addressed (Chapman and Parker 2005). Methods for evaluating the impact of matrix diffusion are addressed in a separate article
Spatial variations in hydraulic conductivity can increase the apparent spreading of solute plumes observed in groundwater monitoring wells. This spreading of the solute caused by large-scale heterogeneities in the aquifer and associated spatial variations in advective transport velocity is referred to as macrodispersion. In some groundwater modeling projects, large values of dispersivity are used as an adjustment factor to help match the apparent large-scale spreading of the plume (ITRC, 2015). Theoretical studies (Gelhar et al. 1979; Gelhar and Axness,1983; Dagan 1988) suggest that macrodispersivity will increase with distance near the source, and then increase more slowly further downgradient, eventually reaching an asymptotic value. Figure 10 shows values of macrodispersivity calculated using the theory of Dagan (1986) with an autocorrelation length of 3 m and several different values of the variance of Y (σ2Y) where Y= Log K. The calculated macrodispersivity increases more rapidly and reaches higher asymptotic values for more heterogeneous aquifers with greater variations in K (larger σ2Y). The maximum predicted dispersivity values are in the range of 0.5 to 5 m.
The ADR equation can be solved to find the spatial and temporal distribution of solutes using a variety of analytical and numerical approaches. The design tools BIOSCREEN[3], BIOCHLOR[4], and REMChlor[5] employ an analytical solution of the ADR equation. MT3DMS[6] uses a numerical method to solve the ADR equation using the head distribution generated by the groundwater flow model MODFLOW[7].
References
- ^ Freeze, A., and Cherry, J., 1979. Groundwater, Prentice-Hall, Englewood Cliffs, New Jersey, 604 pages. Free download from Hydrogeologists Without Borders.
- ^ Woessner, W.W., and Poeter, E.P., 2020. Properties of Earth Materials and Principals of Groundwater Flow, The Groundwater Project, Guelph, Ontario, 207 pages. Free download from The Groundwater Project.
- ^ Newell, C.J., McLeod, R.K. and Gonzales, J.R., 1996. BIOSCREEN: Natural Attenuation Decision Support System - User's Manual, Version 1.3. US Environmental Protection Agency, EPA/600/R-96/087. Report.pdf BIOSCREEN website
- ^ Aziz, C.E., Newell, C.J., Gonzales, J.R., Haas, P.E., Clement, T.P. and Sun, Y., 2000. BIOCHLOR Natural Attenuation Decision Support System. User’s Manual - Version 1.0. US Environmental Protection Agency, EPA/600/R-00/008. Report.pdf BIOCHLOR website
- ^ Falta, R.W., Stacy, M.B., Ahsanuzzaman, A.N.M., Wang, M. and Earle, R.C., 2007. REMChlor Remediation Evaluation Model for Chlorinated Solvents - User’s Manual, Version 1.0. US Environmental Protection Agency. Center for Subsurface Modeling Support, Ada, OK. Report.pdf REMChlor website
- ^ Zheng, C. and Wang, P.P., 1999. MT3DMS: A Modular Three-Dimensional Multispecies Transport Model for Simulation of Advection, Dispersion, and Chemical Reactions of Contaminants in Groundwater Systems; Documentation and User’s Guide. Contract Report SERDP-99-1 U.S. Army Engineer Research and Development Center, Vicksburg, MS. Report.pdf MT3DMS website
- ^ McDonald, M.G. and Harbaugh, A.W., 1988. A Modular Three-dimensional Finite-difference Ground-water Flow Model, Techniques of Water-Resources Investigations, Book 6, Modeling Techniques. U.S. Geological Survey, 586 pages. DOI: 10.3133/twri06A1 Report.pdf Free MODFLOW download from: USGS