User:Jhurley/sandbox
Matrix Diffusion
Matrix Diffusion describes the gradual transport of dissolved contaminants from higher concentration and higher hydraulic conductivity (K) zones of a heterogeneous aquifer into lower K and lower contaminant concentration zones by molecular diffusion. Initially, the transfer of contaminant mass into the low K zones reduces the concentration in the high K zones and slows the migration of the plume. Once the contaminant source is removed and the high K zone contaminant concentration decreases, the contaminants will then diffuse back out of these low K zones. In some cases, matrix diffusion can maintain contaminant concentrations in more permeable zones at greater than target cleanup goals for decades or even centuries after the primary sources have been addressed[1]. Field and laboratory results have illustrated the importance of this process. Analytical and numerical modeling tools are available for evaluating matrix diffusion.
Related Article(s):
Contributors:
Key Resource(s):
Introduction
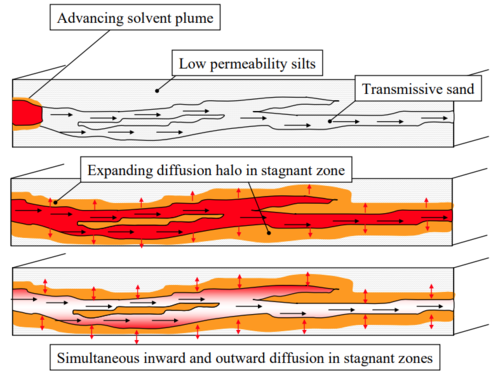
Matrix Diffusion can have major impacts on solute migration in groundwater and on cleanup time following source removal. As a groundwater contaminant plume advances downgradient through a heterogeneous aquifer, some of the dissolved contaminants are transported by molecular diffusion from zones with larger hydraulic conductivity (K) and higher contaminant concentrations into lower K zones with lower concentrations. This transfer of contaminant mass into the low K zones reduces the concentration in the high K zones which slows the rate of contaminant migration in the high K zone. However, once the contaminant source is eliminated and contaminant concentrations in high K zones decrease, the concentration gradient between the high and low conductivity zones is reversed and contaminants will diffuse back out of the low K zones, slowing the cleanup rate in the high K zone (Figure 1). This process, referred to as ‘back diffusion’, can greatly extend cleanup times.
Lab-Scale Studies
The impacts of back diffusion on aquifer cleanup have been examined in controlled laboratory experiments by several investigators[4][5][6][7]. The video in Figure 2 shows the results of a 122-day tracer test in a laboratory flow cell (sand box)[4]. The flow cell contained several clay zones (K = 10-8 cm/s) surrounded by sand (K = 0.02 cm/s). During the loading period, water containing a green fluorescent tracer migrates from left to right with the water flowing through the flow cell, while diffusing into the clay. After 22 days, the fluorescent tracer is eliminated from the feed, and most of the green tracer is quickly flushed from the tank’s sandy zones. However, small amounts of tracer continue to diffuse out of the clay layers for over 100 days. This illustrates how back diffusion of contaminants out of low K zones can maintain low contaminant concentrations long after the contaminant source as been eliminated.
Field Studies
In some cases, matrix diffusion can maintain contaminant concentrations in more permeable zones above target cleanup goals for decades after the primary sources have been addressed. At a site impacted by Dense Non-Aqueous Phase Liquids (DNAPL), trichloroethene (TCE) concentrations in downgradient wells declined by roughly an order-of-magnitude (OoM) when the upgradient source area was isolated with sheet piling. However, after this initial decline, TCE concentrations appeared to plateau or decline more slowly, consistent with back diffusion from an underlying aquitard. Numerical simulations indicated that back diffusion would cause TCE concentrations in downgradient wells at the site to remain above target cleanup levels for centuries[1].
One other implication of matrix diffusion is that plume migration is attenuated by the loss of contaminants into low permeability zones, leading to slower plume migration compared to a case where no matrix diffusion occurs. This phenomena was observed as far back as 1985 when Sudicky et al. observed that “A second consequence of the solute-storage effect offered by transverse diffusion into low-permeability layers is a rate of migration of the frontal portion of a contaminant in the permeable layers that is less than the groundwater velocity.”[8] In cases where there is an attenuating source, matrix diffusion can also reduce the peak concentrations observed in downgradient monitoring wells. The attenuation caused by matrix diffusion may be particularly important for implementing Monitored Natural Attenuation (MNA) for contaminants that do not completely degrade, such as heavy metals and PFAS.
SERPD/ESTCP Research
The SERDP/ESTCP programs have funded several projects focusing on how matrix diffusion can impede progress towards reaching site closure, including:Modeling Matrix Diffusion
Several different modeling approaches have been developed to emulate the diffusive transport of dissolved solutes into and out of lower K zones. The Matrix Diffusion Toolkit[9] is a Microsoft Excel based tool for simulating forward and back diffusion using two different analytical models[12][13]. Numerical models including MODFLOW/MT3DMS[14] have been shown to be effective in simulating back diffusion process and can accurately predict concentration changes over 3 orders-of-magnitude in heterogeneous sand tank experiments[15]. However, numerical models require a fine vertical discretization with short time steps to accurately simulate back diffusion, greatly increasing computation times[16]. These issues can be addressed by incorporating a local 1-D model domain within a general 3D numerical model[17].
The REMChlor - MD toolkit is capable of simulating matrix diffusion in groundwater contaminant plumes by using a semi-analytical method for estimating mass transfer between high and low permeability zones that provides computationally accurate predictions, with much shorter run times than traditional fine grid numerical models[11].
References
- ^ 1.0 1.1 Chapman, S.W. and Parker, B.L., 2005. Plume persistence due to aquitard back diffusion following dense nonaqueous phase liquid source removal or isolation. Water Resources Research, 41(12), Report W12411. DOI: 10.1029/2005WR004224 Report.pdf Free access article from American Geophysical Union
- ^ 2.0 2.1 Sale, T., Parker, B.L., Newell, C.J. and Devlin, J.F., 2013. Management of Contaminants Stored in Low Permeability Zones – A State of the Science Review. Strategic Environmental Research and Development Program (SERDP) Project ER-1740. Report.pdf Website: ER-1740
- ^ Sale, T.C., Illangasekare, T.H., Zimbron, J., Rodriguez, D., Wilking, B., and Marinelli, F., 2007. AFCEE Source Zone Initiative. Air Force Center for Environmental Excellence, Brooks City-Base, San Antonio, TX. Report.pdf
- ^ 4.0 4.1 Doner, L.A., 2008. Tools to resolve water quality benefits of upgradient contaminant flux reduction. Master’s Thesis, Department of Civil and Environmental Engineering, Colorado State University.
- ^ Yang, M., Annable, M.D. and Jawitz, J.W., 2015. Back Diffusion from Thin Low Permeability Zones. Environmental Science and Technology, 49(1), pp. 415-422. DOI: 10.1021/es5045634 Free download available from: ResearchGate
- ^ Yang, M., Annable, M.D. and Jawitz, J.W., 2016. Solute source depletion control of forward and back diffusion through low-permeability zones. Journal of Contaminant Hydrology, 193, pp. 54-62. DOI: 10.1016/j.jconhyd.2016.09.004 Free download available from: ResearchGate
- ^ Tatti, F., Papini, M.P., Sappa, G., Raboni, M., Arjmand, F., and Viotti, P., 2018. Contaminant back-diffusion from low-permeability layers as affected by groundwater velocity: A laboratory investigation by box model and image analysis. Science of The Total Environment, 622, pp. 164-171. DOI: 10.1016/j.scitotenv.2017.11.347
- ^ Sudicky, E.A., Gillham, R.W., and Frind, E.O., 1985. Experimental Investigation of Solute Transport in Stratified Porous Media: 1. The Nonreactive Case. Water Resources Research, 21(7), pp. 1035-1041. DOI: 10.1029/WR021i007p01035
- ^ 9.0 9.1 Farhat, S.K., Newell, C.J., Seyedabbasi, M.A., McDade, J.M., Mahler, N.T., Sale, T.C., Dandy, D.S. and Wahlberg, J.J., 2012. Matrix Diffusion Toolkit. Environmental Security Technology Certification Program (ESTCP) Project ER-201126. User’s Manual.pdf Website: ER-201126
- ^ Sale, T. and Newell, C., 2011. A Guide for Selecting Remedies for Subsurface Releases of Chlorinated Solvents. Environmental Security Technology Certification Program (ESTCP) Project ER-200530. Report.pdf Website: ER-200530
- ^ 11.0 11.1 Farhat, S. K., Newell, C. J., Falta, R. W., and Lynch, K., 2018. A Practical Approach for Modeling Matrix Diffusion Effects in REMChlor. Environmental Security Technology Certification Program (ESTCP) Project ER-201426. User’s Manual.pdf Website: ER-201426
- ^ Parker, B.L., Gillham, R.W., and Cherry, J.A., 1994. Diffusive Disappearance of Immiscible Phase Organic Liquids in Fractured Geologic Media. Groundwater, 32(5), pp. 805-820. DOI: 10.1111/j.1745-6584.1994.tb00922.x
- ^ Sale, T.C., Zimbron, J.A., and Dandy, D.S., 2008. Effects of reduced contaminant loading on downgradient water quality in an idealized two-layer granular porous media. Journal of Contaminant Hydrology, 102(1), pp. 72-85. DOI: 10.1016/j.jconhyd.2008.08.002
- ^ Zheng, C. and Wang, P.P., 1999. MT3DMS: A Modular Three-Dimensional Multispecies Transport Model for Simulation of Advection, Dispersion, and Chemical Reactions of Contaminants in Groundwater Systems; Documentation and User’s Guide. Contract Report SERDP-99-1 U.S. Army Engineer Research and Development Center, Vicksburg, MS. User’s Guide.pdf MT3DMS website
- ^ Chapman, S.W., Parker, B.L., Sale, T.C., Doner, L.A., 2012. Testing high resolution numerical models for analysis of contaminant storage and release from low permeability zones. Journal of Contaminant Hydrology, 136, pp. 106-116. DOI: 10.1016/j.jconhyd.2012.04.006
- ^ Farhat, S.K., Adamson, D.T., Gavaskar, A.R., Lee, S.A., Falta, R.W. and Newell, C.J., 2020. Vertical Discretization Impact in Numerical Modeling of Matrix Diffusion in Contaminated Groundwater. Groundwater Monitoring and Remediation, 40(2), pp. 52-64. DOI: 10.1111/gwmr.12373
- ^ Carey, G.R., Chapman, S.W., Parker, B.L. and McGregor, R., 2015. Application of an Adapted Version of MT3DMS for Modeling Back‐Diffusion Remediation Timeframes. Remediation, 25(4), pp. 55-79. DOI: 10.1002/rem.21440