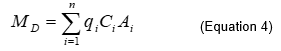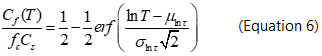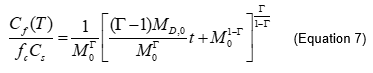Difference between revisions of "Mass Flux and Mass Discharge"

From Enviro Wiki
Jump to: navigation, search
m
m
Line 199: Line 199:
 
| C<sub>S</sub> || is the solubility limit [M/L<sup>3</sup>], and
 
| C<sub>S</sub> || is the solubility limit [M/L<sup>3</sup>], and
 
|-
 
|-
−
| τ (tau) || is the reactive travel time that combines the travel time (t) and the trajectory-averaged DNAPL content that are the mean (&mu;) and standard deviation (&sigma;) of the set of ln(τ) values.  
+
| <nowiki>&tau;</nowiki> (tau) || is the reactive travel time that combines the travel time (t) and the trajectory-averaged DNAPL content that are the mean (&mu;) and standard deviation (&sigma;) of the set of ln(τ) values.  
 
|}
 
|}
  

Revision as of 15:20, 20 August 2018

Use of mass flux and mass discharge measurements for contaminated site management has increased in recent years. Mass flux is the contaminant mass moving across a unit area of porous media (aquifer), while mass discharge is the total mass crossing a control plane of interest, such as the downgradient edge of the source zone or a property boundary. Use of the mass flux/discharge approach combines three different factors: 1) contaminant concentration in groundwater; 2) groundwater flow rate through the site; and 3) size of the source zone. Mass flux and discharge can be estimated using data from monitoring well transects, pumping wells, passive flux meters and other methods. Mass flux and mass discharge can provide site stakeholders a better understanding of the plume behavior, risk, and the relative strength of the source and downgradient plume.


Related Article(s):


Contributor(s): Dr. Michael Annable, P.E.


Key Resource(s):

Introduction

Characterization methods have been developed to measure contaminant mass flux and mass discharge at contaminated sites. This information can be valuable during all phases of site management, including risk assessment, quantifying natural and enhanced attenuation processes, remedial performance assessment, and measuring loads to surface water bodies[1].

Mass flux is defined as the contaminant mass moving across a unit area of porous media (aquifer) perpendicular to the groundwater flow direction and has units of mass/area/time (typically g/m2/day).

Mass discharge is the total mass of contaminant moving across a control plane of interest, such as the downgradient edge of the source zone or a property boundary. The area of interest is generally large enough to contain the entire plume. Units are mass/time (typically g/day or kg/yr).

Mathematics of Mass Flux/Discharge

Consider a simplified site involving a contaminant source from which mass is removed under natural gradient groundwater flow, generating a much larger dissolved contaminant plume. We define mass flux, J [M/L2/T] as the product of the Darcy flux (sometimes called Darcy velocity, see Advection and Groundwater Flow), q [L/T], and the local concentration of contaminant, C [M/L3], in the aqueous phase:

Annable1w2Equation1.PNG

The Darcy flux can be calculated by applying Darcy’s law along the direction of the plume axis at the location of interest:

Annable1w2Equation2.PNG
where:
K is the hydraulic conductivity [L/T] and
dh/dx is the rate of change in hydraulic head with distance at the location of interest.

(Note that seepage velocity which is q divided by the effective porosity, should not be used for mass flux/mass discharge calculations).

For this calculation, the x direction is selected as the direction of groundwater flow. Note that the groundwater flow direction is dynamic and that the contaminant mass flux will change direction with groundwater flow[4]. The contaminant mass flux is a local quantity that can be measured or calculated across a vertical transect into the ground perpendicular to the plume axis. This transect, or control plane, A, then becomes the area over which the local mass flux values are integrated (width and height within the control plane) to quantify mass discharge, MD:

Annable1w2Equation3.PNG

Mass discharge is a scalar quantity in which a positive value reflects contaminant mass transport (also called mass loading) in the direction of groundwater flow. Mass discharge is likely to change with position along the plume axis (typically the x direction and time). Mass discharge measurements quantified near the downgradient edge of the source zone are defined as the source zone mass discharge. How this mass discharge changes with natural dissolution of the source is defined as the source strength function, MD(0,t). Some models for source strength functions are discussed in the Source Zone Models section below.

Related Metric: Site Age
One measure of the site status related to mass flux/discharge is the site age[5]. A simple definition of site age is the fraction of the initial source zone mass that has been removed from the source zone. A site where 90% of the mass has been removed from the source zone would be considered an aged site while those with a small fraction (e.g., 10%) would be considered a young site. Many factors collectively determine how fast a site ages including the solubility limit of the contaminant, the groundwater flow velocity, the size of the source zone in the flow direction, and average non-aqueous phase liquid (NAPL) saturation along the flow path. Sites with a low-solubility dense NAPL (DNAPL), such as tetrachloroethene (PCE) (solubility 150 mg/L), will age more slowly than a comparable site with trichloroethene (TCE) (solubility 1100 mg/L) (see Chlorinated Solvents).

Related Metric: Flux Averaged Concentration
A flux averaged concentration can be calculated for a well simply using C=J/q. This simple approach allows one to relate flux values to target concentration on a flux average basis. Through these basic relationships, targets based on concentration and flux can be linked. If degradation processes are active in the contaminant plume these can be considered and used to lower target remedial objectives for source flux and/or mass discharge.

Methods for Mass Discharge and Mass Flux Measurement

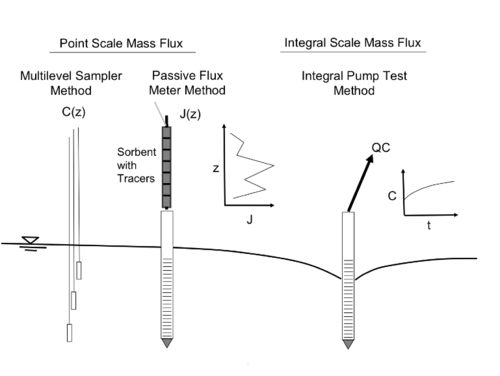
The two general methods for measuring mass flux, J(x,y,z) and mass discharge (MD) based on spatiotemporal scales of measurement (Figure 1) are point scale techniques and integral scale techniques. Point scale techniques include multilevel samplers and passive flux meters within screened wells[6]. Both point scale methods collect data to determine the local mass flux [mass per unit area per time, M/L2/T] that can then be spatially integrated to determine mass discharge [M/T]. Alternatively, integral methods such as integral pump tests[7][8], collect data averaged over large volumes of water pumped from fully screened wells.

Figure 1. Point and integral mass flux methods in wells typically screened 1.5 to 9 m (5 to 30 ft) below ground surface (bgs) with well spacing of 3 to 15 m (10 to 50 ft).

In the most detailed form, mass flux, J(x,y,z), can be calculated using the point scale flux average concentration, C(x,y,z), the point scale hydraulic conductivity, K(x,y,z) and the point scale hydraulic gradient, dh/dx, applied in the direction of groundwater flow. Measuring K and dh/dx at each location can be a major effort. As a result, site-wide average values are often applied for dh/dx and K, while the flux averaged concentration distributions are obtained using multilevel samplers[9]. In this approach, spatial variability is determined for local mass flux that is simply a function of the concentration distribution. Any correlation between the Darcy flux and concentration is not considered.

The Interstate Technology and Regulatory Council’s (ITRC, 2010) “Use and measurement of mass flux and mass discharge” document[1] organized these concepts into five separate methods for obtaining mass flux / mass discharge data. While several methods are related (for example, passive flux meters are often arrayed in a transect), this list presents five different general strategies to generate mass flux/discharge data:

  1. Transect Method
  2. Passive Flux Meters
  3. Well Pumping Methods
  4. Transects Based on Isocontours
  5. Solute Transport Models

Transect Method
The traditional method for calculating contaminant discharge from a NAPL source area or at some location within a plume is called the Transect Method[1][10]. It uses the product of the Darcy flux, the well cross sectional area within a transect of wells, and the contaminant concentration in each well. The Darcy flux can be calculated as the product of independent measures of the hydraulic gradient and hydraulic conductivity. To calculate the contaminant mass flux, groundwater samples are collected from the fully screened wells forming the transect. The contaminant flux is calculated as the product of the Darcy flux for each well and the flux averaged concentration collected from each well.

The transect method also can be applied to a line of multi-level samplers downgradient of the source area or across a plume at a location of interest. In this case, the calculation is made for each sampling location to determine the local mass flux using the local contaminant concentration. The local Darcy flux can only be calculated if the local hydraulic conductivity and hydraulic gradient are measured. The hydraulic conductivity may be available from locally conducted slug tests or borehole flow meter analysis in adjacent screened wells.

Mass discharge across transects can be calculated using a number of methods[1], but in general it can be summarized as:

Annable1w2Equation4.PNG

A free software tool, the Mass Flux Toolkit, was developed by ESTCP (Project ER-200430) to help practitioners perform mass flux/mass discharge calculations[11]. Figure 2 shows the input data and transect construction screen for the Toolkit with example data.

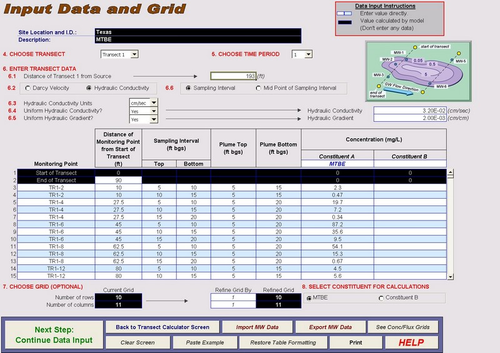
Figure 2. Data input screen for ESTCP Mass Flux Toolkit[11]

Transect mass fluxes can be measured directly using passive flux meters[3][12], multi-level samplers, stochastic methods[13], and combinations of these techniques in addition to others. To obtain mass discharge, spatial interpolation of mass flux data within a transect is required. Methods to calculate mass discharge via multi-level point samplers are described by Kübert and Finkel (2006)[14]. Alternatively, stochastic analysis of the transects’ data may be necessary to improve accuracy and quantify uncertainty[15].

Passive Flux Meters
An alternate approach to measuring groundwater and contaminant fluxes involves deployment of a permeable, sorbent pack (passive flux meter or PFM) inside groundwater wells located along a transect and screened across the vertical extent of the contaminant plume[16][6][3]. The PFM sorbent material is selected to capture the dissolved contaminants in the groundwater as it flows through the flux meter during the designated period of exposure under natural gradient groundwater flow conditions. Thus, flux measurements using this approach are referred to as passive in contrast to methods that require pumping water. PFMs were developed with funding from ESTCP (ESTCP Project ER-0114).

The PFMs placed in wells are pre-saturated with resident tracers that are desorbed or depleted as groundwater flows through the well. Groundwater fluxes are calculated from the depletion of tracer mass, while the mass of contaminants captured on the sorbent is used to estimate contaminant fluxes. By analyzing the sorbent for the residual tracers and the captured contaminants in vertical segments of the PFM, the depth distribution of groundwater and contaminant fluxes along the well screen interval can be determined. Descriptions of the theoretical development for PFM[6], field-scale validation efforts[3], and a field-scale PFM application for site characterization[17] are available in the literature.

The use of PFMs can be optimized by selecting tracers with appropriate retardation on the sorbent used, and by installing the PFMs for a time period such that tracer loss and contaminant mass accumulation are quantifiable. These design parameters are based on existing estimates of the groundwater flux and contaminant concentrations at the site. More advanced interpretation of PFM data is provided by Klammler et al., (2007a, b)[18][19].

Passive flux meters have been used at hundreds of sites for most common volatile organic compound (VOC) contaminants and some nutrients and some metals. One vendor (Enviroflux) can provide passive flux meter devices for down-well deployment at project sites, with optional full laboratory analysis of the subsequently recovered flux meters.

Well Pumping and Integral Pump Tests
A very simple method to measure mass discharge from a plume is to capture the plume with a pumping well. Mass discharge = pumping flowrate x contaminant concentration in extracted groundwater. To use this method, one should make sure that the entire plume is captured, and that the pumping is not changing the source zone water flow leading to enhanced dissolution. The integral pump test (IPT) technique for measuring mass flux or mass discharge is a more sophisticated version of the well pumping approach where contaminant concentration-time series in the effluent of multiple pumping wells aligned perpendicularly to the prevailing direction of groundwater flow are used. Concentration-time series information was initially used to estimate contaminant flux or mass discharge around 2000[20][21], with applications reported shortly thereafter[7][22]. The measured concentration of contaminants is used with independent estimates of the natural gradient Darcy flux. This method is similar to the transect method, but provides an integrated measure of the contaminant flux across the entire well transect and ensures that even very localized high contaminant concentration zones (which might be missed by more discrete methods) are accounted for.

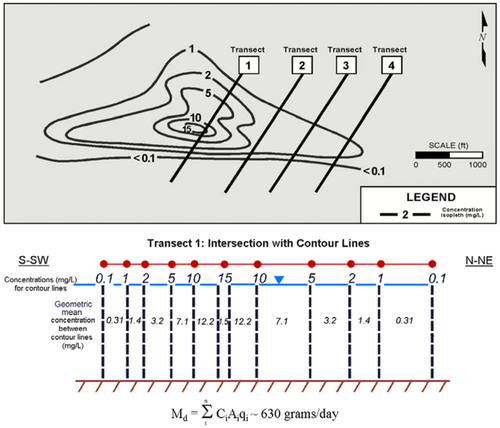
Figure 3. Example of isocontour method to generate synthetic contours based on plume maps[23][1] (adapted from Einarson, 2001)[24].

Transects Based on Isocontours
In this method, well characterized isocontour (plume) maps are used to construct synthetic transects that are then calculated using the methods shown in the transect method. Figure 3 shows an example. While this method is thought to be less powerful by advocates of high-resolution site characterization, the ITRC[1] concluded it is a useful method if the underlying groundwater plume map is based on sufficient and accurate groundwater monitoring data.

Solute Transport Models
Solute transport models directly integrate source size, groundwater flow, and groundwater concentration data. Many models that provide mass flux/mass discharge data are presented in ITRC, 2010[1]. (see also Plume Response Modeling).

Magnitude of Mass Discharge Values

The mass discharge from DNAPL sources can vary over several orders of magnitude between different sites[1][25]. In addition, the mass flux within a given site can vary widely over time and space. For example, a study using multilevel samplers at four sites found a range of integrated mass load estimates ranging from 41 to 85 g/day for TCE, but the individual mass flux values varied enormously over short distances [9].

Newell et al. (2011)[25] developed a contaminant plume classification system based on mass discharge that combined several key concepts and data sources (Table 1):

  • Many classification systems that classify natural phenomena are based on a factor of 10 scale, such as the Richter scale for earthquakes and the Saffir-Simpson hurricane intensity scale.
  • Groundwater hydrology and transport are very much a factor of 10 endeavor, with hydraulic conductivity being discussed as exponents (for example, a particular water bearing unit is a “ten to the minus 2 centimeter per second sand”) and many plume maps drawn with 1, 10, 100, 1000 ug/L contours.
  • In a mass discharge database of 40 sites with a variety of contaminants, the mass discharge ranged from 0.00078 to 56,000 grams per day, a span of eight orders of magnitude.
  • A plume magnitude classification system should therefore be based on mass discharge using a factor of 10 scale.
Table 1. Plume magnitude classification system based on mass discharge. A Mag 1 plume is a low magnitude plume, while a Mag 10 plume is a plume with an exceptionally high mass loading[25].
Mass Discharge
(grams per day) 		Plume
Category
< 0.0001 to 0.001 Mag 1 Plume
0.001 to 0.01 Mag 2 Plume
0.01 to 0.1 Mag 3 Plume
0.1 to 1 Mag 4 Plume
1 to 10 Mag 5 Plume
10 to 100 Mag 6 Plume
100 to 1,000 Mag 7 Plume
1,000 to 10,000 Mag 8 Plume
10,000 to 100,000 Mag 9 Plume
> 100,000 Mag 10 Plume


Using Mass Discharge for Evaluating Risk

Einarson and Mackay (2001)[26] developed a method for applying mass discharge to understand how a contaminant source to groundwater might affect a downgradient water supply well (or surface water receiving body) when mixing with clean water at the point of exposure (the well or the stream) was considered. They produced the following equation to find the contaminant concentration at the receptor (supply well or surface stream) which accounts for the dilution effect due to flow from uncontaminated portions of the aquifer or clean stream flow:

Annable1w2Equation5.PNG
where:
CSW is the contaminant concentration in water extracted from the supply well or stream [M/L3] (e.g., mg/L),
Md is the mass discharge of the plume along the edge of the water supply well capture zone or stream [M/t] (e.g. g/d), and
QSW is the pumping rate of the supply well or flowrate of the surface water stream [L3/t] (e.g., L/d).

The ITRC (2010)[1] provided this example of the Einarson/Mackay equation:

A plume with a mass discharge of 1,000 mg/d TCE (as measured across a transect at the junction of the edges of the plume and the well capture zone) is captured by a domestic well with a pumping rate of 1,000 L/d. The resulting concentration in the domestic water supply would be 1.0 mg/L (1,000 mg/d ÷ 1,000 L/d). However, if the same plume were captured by a large public water supply well pumping 1,000,000 L/d (about 200 gallons per minute [gpm]), then the resulting concentration in water extracted by the water supply well would only be 0.001 mg/L, which is below the maximum contaminant level (MCL) for TCE. While cleanup goals should not rely on blending in a supply well, this example reflects the importance of mass discharge in assessing potential impacts to a receptor, remedial strategies, and prioritizing site cleanups.

The Plume Magnitude Classification system[25] used this approach to determine the minimum magnitude of plume necessary to adversely affect a receptor at a concentration of 5 ug/L (the drinking water standard for many VOC contaminants):

  • Domestic water well pumping 600 liters per day: Mag 2 or larger
  • Municipal water supply well pumping at 400 liters per minute: Mag 5 or larger
  • Stream with mixing zone with flow of 4 cubic meters per second: Mag 8 or larger.

This approach was originally intended to prioritize smaller source zones, where the plumes had not yet reached a receptor well or stream, but has also been used to evaluate the risk to downgradient receptors from different source zones. While both Einarson and Mackay (2001)[26] and the ITRC (2010)[1] stress that dilution should not be relied upon for managing direct exposures, these calculations can be useful for assessing potential impacts to a receptor, remedial strategies, and prioritizing site cleanups.

Source Zone Models that Link Mass Depletion, Mass Flux/Discharge

Site remediation activities often focus on treating the source zone, with the objective of reducing mass discharge to the downgradient aquifer. Measurements in hydraulically isolated test cells and at field sites indicate mass removal from DNAPL source zones can result in significant reductions in mass flux and mass discharge[27][2][28] (see Remediation Performance Assessment). However, laboratory and modeling studies indicate that there is a complex relationship between amount of DNAPL removed and changes in mass discharge, which depends on local hydrogeological conditions and DNAPL distribution.

Several modeling approaches have been developed to relate mass removal from DNAPL source zones to changes in mass discharge or flux[29][30][31][32][33][34][5][35] (also see Source Zone Modeling). Common approaches include analytical source strength function models, the power source depletion model, and DNAPL source zone depletion estimation.

Analytical Source Strength Models
There are simplified analytical source strength function models designed to simulate DNAPL dissolution from source zones. These models have been compared to complex multiphase flow and transport models (see Source Zone Modeling), and results support their use for simple long-term predictions[36]. The equilibrium streamtube model (ESM) is based on an approach in which the DNAPL source zone is conceptualized as a collection of non-interacting streamtubes, with groundwater flow and DNAPL heterogeneity represented by various travel times and DNAPL saturations within different streamtubes[37][5]:

Annable1w2Equation6.png
where:
Cf is the flux-averaged concentration exiting the source zone [M/L3],
T is the number of pore volumes of natural flowing groundwater that have moved through the source zone [-],
fC is the fraction of the streamtubes initially containing DNAPL [-],
CS is the solubility limit [M/L3], and
τ (tau) is the reactive travel time that combines the travel time (t) and the trajectory-averaged DNAPL content that are the mean (μ) and standard deviation (σ) of the set of ln(τ) values.

Power Source Depletion Model
The power law source depletion model (PLM) initially proposed by Rao et al. (2002)[30] is incorporated in the REMCHLOR model[38] and can be used to access the impact of source area remediation on the downgradient plume. The power function relates the flux-averaged concentration to the source mass through an empirical fitting parameter, gamma (Γ) that is a function of both porous media and DNAPL variability. The resulting analytical solution is:

Annable1w2Equation7.PNG
where:
M0 is the initial source mass [M], and
MD,0 is the initial mass discharge [M/T].

The gamma term then defines the shape of the mass discharge vs. groundwater flushing relationship.

DNAPL Source Zone Depletion Estimation
There is a simplified model for estimating DNAPL source zone mass depletion using an effective Damkohler number (Da) approach that considers the groundwater velocity and the size of the NAPL source zone[33]:

Annable1w2Equation8.PNG

In this equation,

Annable1w2Equation9.PNG
where:
keff is the field-scale effective mass transfer coefficient [1/T],
Ls is the source zone length in the mean flow direction [L], and
q is the average Darcy flux (also called Darcy velocity) for the source zone [L/T][33].

The effective mass transfer coefficient (keff) is related to changes in the DNAPL mass and the average groundwater velocity.

Source Models That Link Mass Discharge to Groundwater Flushing
The Equilibrium Streamtube Model and the Power Law Model can be used to show how mass discharge from a DNAPL source zone changes as more water flushes through the source zone (Fig. 4). The most simplified case is a constant mass discharge over many pore flushes where the gamma term in the Power Law Model is gamma = 0 (after Sale and McWhorter (2001)[29], see Fig. 1). However, this case is only representative of a domain with a homogeneous groundwater flow field and uniform DNAPL distribution in the source zone[31]. The other extreme case is for very high values of gamma in which case the mass discharge declines rapidly early on in the flushing process, but has extreme tailing behavior (flattening of the mass discharge vs. pore volume curve). This behavior is expected from sites with high geologic heterogeneities that cause long tailing from limited DNAPL pools or release from back-diffusion zones.

Figure 4. Power Law model for source zone dissolution showing different values of gamma (Γ)

Fitting a Source Zone Model to Mass Flux/Discharge Data
The source zone models are used in two ways: 1) the source zone parameters can be estimated or 2) the source model can be fit to actual mass flux/discharge data at a site. For an example of the first approach with the Power Law Model, the value of gamma is often close to 1, and typically ranges from ~ 0.5 to 2, with higher values associated with sites affected by matrix diffusion (see Source Zone Modeling). Several methods are presented below for using site specific data in a source zone model.

Using Computer Models: At field sites that have undergone years of investigation, there are generally a number of well locations at varying depths throughout the plume and source zones. To take advantage of these data in an effort to characterize source zone behavior, a plume matching technique can be employed by coupling an advection-dispersion model with a source-strength function as a concentration boundary condition. Ideally, this method would employ an advanced, calibrated site groundwater flow model.

As solute migrates away from the source zone into the contaminant plume, the contaminant concentration can be affected by a number of processes other than source zone behavior (biodegradation, sorption, diffusion and volatilization). For this reason, wells near the source zone are considered to more directly reflect the source zone behavior than those farther from the source zone

Using Time Series Data: Two approaches can be used to fit an unknown source strength function to concentration time series field data. The first is a global fit to all data trying to optimize the function parameters in the model. While ideally the entire plume response (all available data) would be fit to a single set of source-strength function parameters, in reality a distribution of parameters that best describes the plume response at a field site is probable. A second approach is the use of individual wells to fit source strength function parameters. While the uncertainty is much higher for each individual well fit, the distribution of parameter values can be used to estimate a range of likely values.

Using Temporal Transects: Because well transects can be used to couple flux-averaged concentration with groundwater flow to produce mass flux and integrated mass-discharge values, observing the change in these flux values in time can produce a meaningful mass-discharge time series that: 1) indicate how the source attenuates over time and 2) can be directly fit to source strength functions.

Using Spatial Transects: Transect data collection in space involves having multiple well transects at significant distance separation down the plume centerline. This allows for translation of concentrations in time without the need of significantly long time series data. This translation from space to time is done via travel time using assumed retardation and groundwater velocity between transects. Careful consideration must be made to quantify any losses, such as complete degradation of the product, changes in hydro-stratigraphy between transects, and remediation. These data show how the plume attenuates as the plume migrates downgradient.

Using Extraction Wells: The final method is the evaluation of source strength function using changes in extraction well concentration data. This method allows prediction of removal efficiencies and analysis of source behavior changes over time during remedial operations. While fitting a source strength function to the cumulative mass removal of these data is possible, the source strength functions that describe this pumping may not accurately reflect the source strength function under natural groundwater gradients.

Remedial Considerations

The underlying goal of source zone or DNAPL treatment is to reduce the risks posed by the contamination to humans and the environment. Aqueous contaminant concentrations can be viewed as surrogate measures of risk, and are often the primary metric for regulatory decisions. Under this traditional framework, the goal for NAPL source treatment technologies is to achieve acceptable aqueous concentrations such as drinking water standards by either removing or destroying NAPL mass in the source zone. Unfortunately, current NAPL remedial technologies are unable to completely eliminate NAPL from source areas at all sites, and partial mass removal from NAPL source zones is unlikely to be sufficient to meet drinking water standards at all locations within a site. Other potential benefits may, however, be achieved as a result of source treatment, and one proposed benefit is a reduction in contaminant mass discharge (M/T) from the NAPL source area[30][39][40][41][42] (see Remediation Performance Assessment). The magnitude of the benefit realized needs to be quantified by measuring mass flux and discharge before and after remedial efforts are implemented.

Flux measurements should be conducted using the same protocol before and after remedial treatment, and differences in hydrologic conditions should be considered when interpreting the data. Also critical is the need to provide adequate time between the remedial activity and the post-remedial flux measurement to ensure that conditions are representative of natural groundwater flow and contaminant dissolution from the original source area. Too often there is a rush to measure the effect of the remedial action, and the measurements are only indicative of modifications still significantly influenced by remedial actions such as elevated temperatures or residual flushing agents. A general rule may be to require at least two pore volumes of natural gradient water flow to pass through the source area extending to the monitoring location prior to post-remedial monitoring of mass flux. For many sites this could mean two to five years following remediation. Often site managers may find this length of time unacceptable. Partly for this reason, very few studies have been completed to date with high quality measurements of pre- and post-remediation flux measurements[2].

Summary

Mass flux and mass discharge represent a new way to evaluate and think about contaminant plumes. Instead of assuming that every liter of groundwater must be cleaned up to a certain standard, even if this water is in clays or silts or other low permeability zones, the mass flux/discharge approach evaluates risk by combining the source size, groundwater velocity, and groundwater concentrations. There are five general methods for measuring mass flux/discharge[1]: Transect Method, Well Pumping Methods, Passive Flux Meters, Transects Based on Isocontours, and Solute Transport Models.

Mass flux/discharge data can be used for assessing potential impacts to a receptor, designing remedial strategies, and prioritizing site cleanups[1]. In particular, the risk of a source to a potential downgradient receptor at a well or stream can be estimated by dividing the mass discharge from the source or plume by the flowrate associated with the well or the stream. This provides a concentration that includes the clean water mixed with the discharge from the plume. Mass flux/discharge data can also be used to calibrate source zone models that link mass flux/discharge to groundwater flushing, thereby showing how the mass discharge from a contaminant source will change as the source ages.

References

  1. ^ 1.00 1.01 1.02 1.03 1.04 1.05 1.06 1.07 1.08 1.09 1.10 1.11 1.12 Interstate Technology & Regulatory Council (ITRC), 2010. Use and Measurement of Mass Flux and Mass Discharge. Integrated DNAPL Site Strategy Team, The Interstate Technology & Regulatory Council, p.154. Report.pdf
  2. ^ 2.0 2.1 2.2 Brooks, M.C., Wood, A.L., Annable, M.D., Hatfield, K., Cho, J., Holbert, C., Rao, P.S.C., Enfield, C.G., Lynch, K. and Smith, R.E., 2008. Changes in contaminant mass discharge from DNAPL source mass depletion: Evaluation at two field sites. Journal of Contaminant Hydrology, 102(1-2), pp.140-153. doi: 10.1016/j.jconhyd.2008.05.008 Report.pdf
  3. ^ 3.0 3.1 3.2 3.3 Annable, M.D., Hatfield, K., Cho, J., Klammler, H., Parker, B.L., Cherry, J.A. and Rao, P.S.C., 2005. Field-scale evaluation of the passive flux meter for simultaneous measurement of groundwater and contaminant fluxes. Environmental science & technology, 39(18), pp.7194-7201. doi: 10.1021/es050074g Report.pdf
  4. ^ Rein, A., Bauer, S., Dietrich, P. and Beyer, C., 2009. Influence of temporally variable groundwater flow conditions on point measurements and contaminant mass flux estimations. Journal of contaminant hydrology, 108(3-4), pp.118-133. doi: 10.1016/j.jconhyd.2009.06.005
  5. ^ 5.0 5.1 5.2 Jawitz, J.W., Fure, A.D., Demmy, G.G., Berglund, S. and Rao, P.S.C., 2005. Groundwater contaminant flux reduction resulting from nonaqueous phase liquid mass reduction. Water Resources Research, 41(10). doi: 10.1029/2004WR003825 Report.pdf
  6. ^ 6.0 6.1 6.2 Hatfield, K., Annable, M., Cho, J., Rao, P.S.C. and Klammler, H., 2004. A direct passive method for measuring water and contaminant fluxes in porous media. Journal of Contaminant Hydrology, 75(3-4), pp.155-181. doi: 10.1016/j.jconhyd.2004.06.005 Report.pdf
  7. ^ 7.0 7.1 Bockelmann, A., Ptak, T. and Teutsch, G., 2001. An analytical quantification of mass fluxes and natural attenuation rate constants at a former gasworks site. Journal of Contaminant Hydrology, 53(3-4), pp.429-453. doi: 10.1016/S0169-7722(01)00177-2
  8. ^ Goltz, M.N., Huang, J., Close, M.E., Flintoft, M.J. and Pang, L., 2008. Use of tandem circulation wells to measure hydraulic conductivity without groundwater extraction. Journal of contaminant hydrology, 100(3-4), pp.127-136. doi: 10.1016/j.jconhyd.2008.06.003
  9. ^ 9.0 9.1 Guilbeault, M.A., Parker, B.L. and Cherry, J.A., 2005. Mass and flux distributions from DNAPL zones in sandy aquifers. Groundwater, 43(1), pp.70-86. doi: 10.1111/j.1745-6584.2005.tb02287.x report.pdf
  10. ^ Newell, C.J., Conner, J.A. and Rowen, D.L., 2003. Groundwater remediation strategies tool. Prepared for American Petroleum Institute, Regulatory Analysis and Scientific Affairs Department, Publication, (4730). Report.pdf
  11. ^ 11.0 11.1 Farhat, S.K., Newell, C.J. and Nichols, E.M., 2006. Mass Flux Toolkit to Evaluate Groundwater Impacts, Attenuation, and Remediation Alternatives. User's Manual. GSI Environmental Inc, Houston, Tx. ER-200430
  12. ^ Basu, N.B., Fure, A.D. and Jawitz, J.W., 2008. Simplified contaminant source depletion models as analogs of multiphase simulators. Journal of Contaminant Hydrology, 97(3-4), pp.87-99. doi: 10.1016/j.jconhyd.2008.01.001
  13. ^ Schwede, R.L. and Cirpka, O.A., 2009. Use of steady-state concentration measurements in geostatistical inversion. Advances in Water Resources, 32(4), pp.607-619. doi: 10.1016/j.advwatres.2009.01.010
  14. ^ Kübert, M. and Finkel, M., 2006. Contaminant mass discharge estimation in groundwater based on multi-level point measurements: A numerical evaluation of expected errors. Journal of contaminant hydrology, 84(1-2), pp.55-80. doi: 10.1016/j.jconhyd.2005.12.003
  15. ^ Klammler, H., Hatfield, K., Guimarães da Luz, J.A., Annable, M.D., Newman, M., Cho, J., Peacock, A., Stucker, V., Ranville, J., Cabaniss, S.A. and Rao, P.S.C., 2012. Contaminant discharge and uncertainty estimates from passive flux meter measurements. Water Resources Research, 48(2). doi:10.1029/2011WR010535. Report.pdf
  16. ^ Hatfield, K., Rao, P.S.C., Annable, M.D. and Campbell, T.J., University of Florida, 2002. Device and method for measuring fluid and solute fluxes in flow systems. U.S. Patent 6,401,547. Report.pdf
  17. ^ Basu, N.B., Rao, P.S.C., Poyer, I.C., Annable, M.D. and Hatfield, K., 2006. Flux-based assessment at a manufacturing site contaminated with trichloroethylene. Journal of Contaminant Hydrology, 86(1-2), pp.105-127. doi: 10.1016/j.jconhyd.2006.02.011
  18. ^ Klammler, H., Hatfield, K. and Annable, M.D., 2007. Concepts for measuring horizontal groundwater flow directions using the passive flux meter. Advances in Water Resources, 30(4), pp.984-997. Report.pdf
  19. ^ Klammler, H., Hatfield, K., Annable, M.D., Agyei, E., Parker, B.L., Cherry, J.A. and Rao, P.S.C., 2007. General analytical treatment of the flow field relevant to the interpretation of passive fluxmeter measurements. Water Resources Research, 43(4). doi:10.1029/2005WR004718 Report.pdf
  20. ^ Teutsch, G., Ptak, T., Schwarz, R. and Holder, T., 2000. Ein neues integrales Verfahren zur Quantifizierung der Grundwasserimmission, Teil I: Beschreibung der Grundlagen. Grundwasser, 5(4), pp.170-175.
  21. ^ Ptak, T., Schirmer, M. and Teutsch, G., 2000. Development and performance of a new multilevel groundwater sampling system. In Second International Conference on Remediation of Chlorinated and Recalcitrant Compounds. Battelle Press, Columbus, OH, USA (pp. 95-102)
  22. ^ Bockelmann, A., Zamfirescu, D., Ptak, T., Grathwohl, P. and Teutsch, G., 2003. Quantification of mass fluxes and natural attenuation rates at an industrial site with a limited monitoring network: a case study. Journal of Contaminant Hydrology, 60(1-2), pp.97-121. doi: 10.1016/S0169-7722(02)00060-8
  23. ^ Newell, C.J., Conner, J.A. and Rowen, D.L., 2003. Groundwater remediation strategies tool. Prepared for American Petroleum Institute, Regulatory Analysis and Scientific Affairs Department, Publication, (4730).
  24. ^ Einarson, M.D., 2001. Flux-Based Corrective Action. Princeton Groundwater Remediation Course. Denver, Colorado.
  25. ^ 25.0 25.1 25.2 25.3 Newell, Charles J., Shahla K. Farhat, David T. Adamson, and Brian B. Looney. "Contaminant plume classification system based on mass discharge." Groundwater 49, no. 6 (2011): 914-919. doi: 10.1111/j.1745-6584.2010.00793.x
  26. ^ 26.0 26.1 Einarson, M.D. and Mackay, D.M., 2001. Peer reviewed: predicting impacts of groundwater contamination. Environ Sci Technol 35(3) pp. 66A-73A. Report.pdf
  27. ^ Brooks, M.C., Annable, M.D., Rao, P.S.C., Hatfield, K., Jawitz, J.W., Wise, W.R., Wood, A.L. and Enfield, C.G., 2004. Controlled release, blind test of DNAPL remediation by ethanol flushing. Journal of Contaminant Hydrology, 69(3-4), pp.281-297. doi: 10.1016/S0169-7722(03)00158-X
  28. ^ DiFilippo, E.L. and Brusseau, M.L., 2008. Relationship between mass-flux reduction and source-zone mass removal: analysis of field data. Journal of Contaminant Hydrology, 98(1-2), pp.22-35. doi: 10.1016/j.jconhyd.2008.02.004 Report.pdf
  29. ^ 29.0 29.1 Sale, T.C. and McWhorter, D.B., 2001. Steady state mass transfer from single‐component dense nonaqueous phase liquids in uniform flow fields. Water Resources Research, 37(2), pp.393-404. doi: 10.1029/2000WR900236 Report.pdf
  30. ^ 30.0 30.1 30.2 Rao, P.S.C., Jawitz, J.W., Enfield, C.G., Falta Jr, R.W., Annable, M.D. and Wood, A.L., 2001. Technology integration for contaminated site remediation: clean-up goals and performance criteria. Groundwater quality: Natural and enhanced restoration of groundwater pollution, 275, pp.571-578. Report.pdf
  31. ^ 31.0 31.1 Rao, P.S.C. and Jawitz, J.W., 2003. Comment on “Steady state mass transfer from single‐component dense nonaqueous phase liquids in uniform flow fields” by TC Sale and DB McWhorter. Water Resources Research, 39(3). doi: 10.1029/2001WR000599
  32. ^ Lemke, L.D., Abriola, L.M. and Lang, J.R., 2004. Influence of hydraulic property correlation on predicted dense nonaqueous phase liquid source zone architecture, mass recovery and contaminant flux. Water Resources Research, 40(12). doi:10.1029/2004WR003061 Report.pdf
  33. ^ 33.0 33.1 33.2 Parker, J.C. and Park, E., 2004. Modeling field‐scale dense nonaqueous phase liquid dissolution kinetics in heterogeneous aquifers. Water Resources Research, 40(5). doi: 10.1029/2003WR002807
  34. ^ Enfield, C.G., Wood, A.L., Espinoza, F.P., Brooks, M.C., Annable, M. and Rao, P.S.C., 2005. Design of aquifer remediation systems:(1) Describing hydraulic structure and NAPL architecture using tracers. Journal of Contaminant Hydrology, 81(1-4), pp.125-147. doi: 10.1016/j.jconhyd.2005.08.003
  35. ^ Wood, A.L., Enfield, C.G., Espinoza, F.P., Annable, M., Brooks, M.C., Rao, P.S.C., Sabatini, D. and Knox, R., 2005. Design of aquifer remediation systems:(2) Estimating site-specific performance and benefits of partial source removal. Journal of contaminant hydrology, 81(1-4), pp.148-166. doi: 10.1016/j.jconhyd.2005.08.004
  36. ^ Basu, N.B., Fure, A.D. and Jawitz, J.W., 2008. Simplified contaminant source depletion models as analogs of multiphase simulators. Journal of Contaminant Hydrology, 97(3-4), pp.87-99. doi: 10.1016/j.jconhyd.2008.01.001
  37. ^ Jawitz, J.W., Annable, M.D., Demmy, G.G. and Rao, P.S.C., 2003. Estimating nonaqueous phase liquid spatial variability using partitioning tracer higher temporal moments. Water Resources Research, 39(7) p.1192. doi: 10.1029/2002WR001309 Report.pdf
  38. ^ Falta, R.W., Rao, P.S. and Basu, N., 2005. Assessing the impacts of partial mass depletion in DNAPL source zones: I. Analytical modeling of source strength functions and plume response. Journal of Contaminant Hydrology, 78(4), pp.259-280. doi: 10.1016/j.jconhyd.2005.05.010
  39. ^ Kavanaugh, M.C., Suresh, P. and Rao, C., 2003. The DNAPL remediation challenge: Is there a case for source depletion? National Risk Management Research Laboratory, Office of Research and Development, U.S. Environmental Progtection Agency, Cincinnati, OH, USA. EPA/600/R-03/143. Report.pdf
  40. ^ Stroo, H.F., Unger, M., Ward, C.H., Kavanaugh, M.C., Vogel, C., Leeson, A., Marqusee, J.A. and Smith, B.P., 2003. Peer reviewed: Remediating chlorinated solvent source zones. Environ. Sci Technol. 37 (11), pp 224A–230A. doi: 10.1021/es032488k Report.pdf
  41. ^ ITRC (Interstate Technology & Regulatory Council). 2003. Assessing the performance of DNAPL source reduction remedies. Dense Nonaqueous Phase Liquids Team, Washington, DC, USA
  42. ^ National Research Council, 2005. Contaminants in the subsurface: Source zone assessment and remediation. National Academies Press. Report.pdf


See Also

Retrieved from "https://www.enviro.wiki/index.php?title=Mass_Flux_and_Mass_Discharge&oldid=11974"