User:Jhurley/sandbox
Advection and Groundwater Flow
Groundwater migrates from areas of higher hydraulic head (a measure of pressure and gravitational energy) toward lower hydraulic head, transporting dissolved solutes through the combined processes of advection and dispersion. Advection refers to the bulk movement of solutes carried by flowing groundwater. Dispersion refers to the spreading of the contaminant plume from highly concentrated areas to less concentrated areas. In many groundwater transport models, solute transport is described by the advection-dispersion-reaction equation.
Related Article(s):
CONTRIBUTOR(S):
Key Resource(s):
- Groundwater[1], Freeze and Cherry, 1979.
- Hydrogeologic Properties of Earth Materials and Principals of Groundwater Flow[2], Woessner and Poeter, 2020.
Groundwater Flow

Groundwater flows from areas of higher hydraulic head toward areas of lower hydraulic head (Figure 1). The rate of change (slope) of the hydraulic head is known as the hydraulic gradient. If groundwater is flowing and contains dissolved contaminants it can transport the contaminants from areas with high hydraulic head toward lower hydraulic head zones, or “downgradient”.
Darcy's Law
| Aquifer Material | Total Porosity (dimensionless) |
Effective Porosity (dimensionless) |
Hydraulic Conductivity (meters/second) |
|---|---|---|---|
| Unconsolidated | |||
| Gravel | 0.25 — 0.44 | 0.13 — 0.44 | 3×10-4 — 3×10-2 |
| Coarse Sand | 0.31 — 0.46 | 0.18 — 0.43 | 9×10-7 — 6×10-3 |
| Medium Sand | — | 0.16 — 0.46 | 9×10-7 — 5×10-4 |
| Fine Sand | 0.25 — 0.53 | 0.01 — 0.46 | 2×10-7 — 2×10-4 |
| Silt, Loess | 0.35 — 0.50 | 0.01 — 0.39 | 1×10-9 — 2×10-5 |
| Clay | 0.40 — 0.70 | 0.01 — 0.18 | 1×10-11 — 4.7×10-9 |
| Sedimentary and Crystalline Rocks | |||
| Karst and Reef Limestone | 0.05 — 0.50 | — | 1×10-6 — 2×10-2 |
| Limestone, Dolomite | 0.00 — 0.20 | 0.01 — 0.24 | 1×10-9 — 6×10-6 |
| Sandstone | 0.05 — 0.30 | 0.10 — 0.30 | 3×10-10 — 6×10-6 |
| Siltstone | — | 0.21 — 0.41 | 1×10-11 — 1.4×10-8 |
| Basalt | 0.05 — 0.50 | — | 2×10-11 — 2×10-2 |
| Fractured Crystalline Rock | 0.00 — 0.10 | — | 8×10-9 — 3×10-4 |
| Weathered Granite | 0.34 — 0.57 | — | 3.3×10-6 — 5.2×10-5 |
| Unfractured Crystalline Rock | 0.00 — 0.05 | — | 3×10-14 — 2×10-10 |
In unconsolidated geologic settings (gravel, sand, silt, and clay) and highly fractured systems, the rate of groundwater movement can be expressed using Darcy’s Law. This law is a fundamental mathematical relationship in the groundwater field and can be expressed this way:
- Where:
- Q = Flow rate (Volume of groundwater flow per time, such as m3/yr)
- A = Cross sectional area perpendicular to groundwater flow (length2, such as m2)
- VD = “Darcy Velocity”; describes groundwater flow as the volume of flow through a unit of cross-sectional area (units of length per time, such as ft/yr)
- K = Hydraulic Conductivity (sometimes called “permeability”) (length per time)
- ΔH = Difference in hydraulic head between two lateral points (length)
- ΔL = Distance between two lateral points (length)
- Where:
Hydraulic conductivity (Table 1 and Figure 2) is a measure of how easily groundwater flows through a porous medium, or alternatively, how much energy it takes to force water through a porous medium. For example, fine sand has smaller pores with more frictional resistance to flow, and therefore lower hydraulic conductivity compared to coarse sand, which has larger pores with less resistance to flow (Figure 2).

Darcy’s Law was first described by Henry Darcy (1856)[6] in a report regarding a water supply system he designed for the city of Dijon, France. Based on his experiments, he concluded that the amount of water flowing through a closed tube of sand (dark grey box in Figure 3) depends on (a) the change in the hydraulic head between the inlet and outlet of the tube, and (b) the hydraulic conductivity of the sand in the tube. Groundwater flows rapidly in the case of higher pressure (ΔH) or more permeable materials such as gravel or coarse sand, but flows slowly when the pressure is lower or the material is less permeable, such as fine sand or silt.
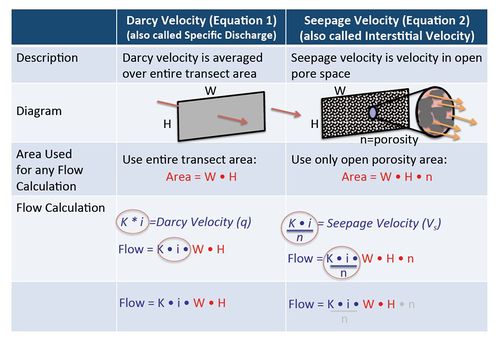
Since Darcy’s time, Darcy’s Law has been adapted to calculate the actual velocity that the groundwater is moving in units such as meters traveled per year. This quantity is called “interstitial velocity” or “seepage velocity” and is calculated by dividing the Darcy Velocity (flow per unit area) by the actual open pore area where groundwater is flowing, the “effective porosity” (Table 1):
- Where:
- VS = “interstitial velocity” or “seepage velocity” (units of length per time, such as m/sec)
- VD = “Darcy Velocity”; describes groundwater flow as the volume of flow per unit area (units of length per time)
- ne = Effective porosity (unitless)
- VS = “interstitial velocity” or “seepage velocity” (units of length per time, such as m/sec)
Effective porosity is smaller than total porosity. The difference is that total porosity includes some dead-end pores that do not support groundwater. Typically values for total and effective porosity are shown in Table 1.
Darcy Velocity and Seepage Velocity
In groundwater calculations, Darcy Velocity and Seepage Velocity are used for different purposes. For any calculation where the actual flow rate in units of volume per time (such as liters per day or gallons per minute) is involved, then the original Darcy Equation should be used (calculate VD; Equation 1) without using effective porosity. When calculating solute travel time, then the seepage velocity calculation (VS; Equation 2) must be used and an estimate of effective porosity is required. Figure 4 illustrates the differences between Darcy Velocity and Seepage Velocity.
Mobile Porosity
| Aquifer Material | Mobile Porosity (volume fraction) |
|---|---|
| Poorly sorted sand and gravel | 0.085 |
| Poorly sorted sand and gravel | 0.04 — 0.07 |
| Poorly sorted sand and gravel | 0.09 |
| Fractured sandstone | 0.001 — 0.007 |
| Alluvial formation | 0.102 |
| Glacial outwash | 0.145 |
| Weathered mudstone regolith | 0.07 — 0.10 |
| Alluvial formation | 0.07 |
| Alluvial formation | 0.07 |
| Silty sand | 0.05 |
| Fractured sandstone | 0.0008 — 0.001 |
| Alluvium, sand and gravel | 0.017 |
| Alluvium, poorly sorted sand and gravel | 0.003 — 0.017 |
| Alluvium, sand and gravel | 0.11 — 0.18 |
| Siltstone, sandstone, mudstone | 0.01 — 0.05 |
Payne et al. (2009) reported the results from multiple short-term tracer tests conducted to aid the design of amendment injection systems[7]. In these tests, the dissolved solutes were observed to migrate more rapidly through the aquifer than could be explained with typically reported values of ne. They concluded that the heterogeneity of unconsolidated formations results in a relatively small area of an aquifer cross section carrying most of the water, and therefore solutes migrate more rapidly than expected. Based on these results, they recommend that a quantity called “mobile porosity” should be used in place of ne in equation 2 for calculating solute transport velocities. Based on 15 different tracer tests, typical values of mobile porosity range from 0.02 to 0.10 (Table 2).
A data mining analysis of 43 sites in California by Kulkarni et al. (2020) showed that on average 90% of the groundwater flow occurred in about 30% of cross sectional area perpendicular to groundwater flow. These data provided “moderate (but not confirmatory) support for the mobile porosity concept.”[8]
Advection-Dispersion-Reaction Equation for Solute Transport
The transport of dissolved solutes in groundwater is often modeled using the Advection-Dispersion-Reaction (ADR) equation. Advection refers to the bulk movement of solutes carried by flowing groundwater. Dispersion refers to the spreading of the contaminant plume from highly concentrated areas to less concentrated areas. Dispersion coefficients are calculated as the sum of molecular diffusion mechanical dispersion, and macrodispersion. Reaction refers to changes in mass of the solute within the system resulting from biotic and abiotic processes.
Related Article(s):
- Advection and Groundwater Flow
- Dispersion and Diffusion
- Sorption of Organic Contaminants
- Plume Response Modeling
CONTRIBUTOR(S):
Key Resource(s):
The ADR Equation
In many groundwater transport models, solute transport is described by the advection-dispersion-reaction equation. As shown below (Equation 3), the ADR equation describes the change in dissolved solute concentration (C) over time (t) where groundwater flow is oriented along the x direction.
- Where:
- R is the linear, equilibrium retardation factor (see Sorption of Organic Contaminants),
- Dx, Dy, and Dz are hydrodynamic dispersion coefficients in the x, y and z directions (L2/T),
- v is the advective transport or seepage velocity in the x direction (L/T), and
- λ is an effective first order decay rate due to combined biotic and abiotic processes (1/T).
The term on the left side of the equation is the rate of mass change per unit volume. On the right side are terms representing the solute flux due to dispersion in the x, y, and z directions, the advective flux in the x direction, and the first order decay due to biotic and abiotic processes. Dispersion coefficients (Dx,y,z) are commonly estimated using the following relationships:
- Where:
- Dm is the molecular diffusion coefficient (L2/T), and
- αL, αT, and αV are the longitudinal, transverse and vertical dispersivities (L).
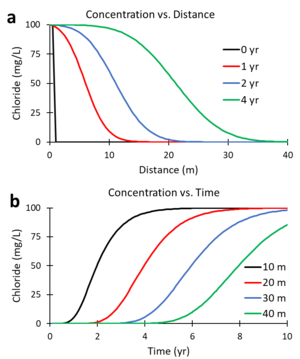
Figures 5a and 5b were generated using a numerical solution of the ADR equation for a non-reactive tracer (R = 1; λ = 0) with v = 5 m/yr and Dx = 10 m2/yr. Figure 5a shows the predicted change in concentration of the tracer, chloride, versus distance downgradient from the continuous contaminant source at different times (0, 1, 2, and 4 years). Figure 5b shows the change in concentration versus time (commonly referred to as the breakthrough curve or BTC) at different downgradient distances (10, 20, 30 and 40 m). At 2 years, the mid-point of the concentration versus distance curve (Figure 5a) is located 10 m downgradient (x = 5 m/yr * 2 yr). At 20 m downgradient, the mid-point of the concentration versus time curves (Figure 5b) occurs at 4 years (t = 20 m / 5 m/yr).
The dispersion coefficient in the ADR equation accounts for the combined effects of molecular diffusion and mechanical dispersion which cause the spreading of the contaminant plume from highly concentrated areas to less concentrated areas. Molecular diffusion is the result of the thermal motion of individual molecules which causes a flux of dissolved solutes from areas of higher concentration to areas of lower concentration. Mechanical dispersion (hydrodynamic dispersion) results from groundwater moving at rates that vary from the average linear velocity. Because the invading solute-containing water does not travel at the same velocity everywhere, mixing occurs along flow paths. Typical values of the mechanical dispersivity measured in laboratory column tests are on the order of 0.01 to 1 cm (Anderson and Cherry, 1979).
Matrix Diffusion is the process where dissolved contaminants are transported into low K zones by molecular diffusion, and then can diffuse back out of these low K zones once the contaminant source is removed. In some cases, matrix diffusion can maintain contaminant concentrations in more permeable zones above target cleanup goals for decades or even centuries after the primary sources have been addressed (Chapman and Parker 2005). Methods for evaluating the impact of matrix diffusion are addressed in a separate article
Spatial variations in hydraulic conductivity can increase the apparent spreading of solute plumes observed in groundwater monitoring wells. This spreading of the solute caused by large-scale heterogeneities in the aquifer and associated spatial variations in advective transport velocity is referred to as macrodispersion. In some groundwater modeling projects, large values of dispersivity are used as an adjustment factor to help match the apparent large-scale spreading of the plume (ITRC, 2015). Theoretical studies (Gelhar et al. 1979; Gelhar and Axness,1983; Dagan 1988) suggest that macrodispersivity will increase with distance near the source, and then increase more slowly further downgradient, eventually reaching an asymptotic value. Figure 10 shows values of macrodispersivity calculated using the theory of Dagan (1986) with an autocorrelation length of 3 m and several different values of the variance of Y (σ2Y) where Y= Log K. The calculated macrodispersivity increases more rapidly and reaches higher asymptotic values for more heterogeneous aquifers with greater variations in K (larger σ2Y). The maximum predicted dispersivity values are in the range of 0.5 to 5 m.
The ADR equation can be solved to find the spatial and temporal distribution of solutes using a variety of analytical and numerical approaches. The design tools BIOSCREEN[9], BIOCHLOR[10], and REMChlor[11] employ an analytical solution of the ADR equation. MT3DMS[12] uses a numerical method to solve the ADR equation using the head distribution generated by the groundwater flow model MODFLOW[13].
References
- ^ 1.0 1.1 Freeze, A., and Cherry, J., 1979. Groundwater, Prentice-Hall, Englewood Cliffs, New Jersey, 604 pages. Free download from Hydrogeologists Without Borders.
- ^ Woessner, W.W., and Poeter, E.P., 2020. Properties of Earth Materials and Principals of Groundwater Flow, The Groundwater Project, Guelph, Ontario, 207 pages. Free download from The Groundwater Project.
- ^ Domenico, P.A. and Schwartz, F.W., 1997. Physical and Chemical Hydrogeology, 2nd Ed. John Wiley & Sons, 528 pgs. ISBN 978-0-471-59762-9. Available from: Wiley
- ^ McWhorter, D.B. and Sunada, D.K., 1977. Ground-water hydrology and hydraulics. Water Resources Publications, LLC, Highlands Ranch, Colorado, 304 pgs. ISBN-13: 978-1-887201-61-2 Available from: Water Resources Publications
- ^ Heath, R.C., 1983. Basic ground-water hydrology, U.S. Geological Survey Water-Supply Paper 2220, 86 pgs. Report pdf
- ^ Brown, G.O., 2002. Henry Darcy and the making of a law. Water Resources Research, 38(7), p. 1106. DOI: 10.1029/2001WR000727 Report.pdf
- ^ 7.0 7.1 Payne, F.C., Quinnan, J.A. and Potter, S.T., 2008. Remediation Hydraulics. CRC Press. ISBN 9780849372490 Available from: CRC Press
- ^ Kulkarni, P.R., Godwin, W.R., Long, J.A., Newell, R.C., Newell, C.J., 2020. How much heterogeneity? Flow versus area from a big data perspective. Remediation 30(2), pp. 15-23. DOI: 10.1002/rem.21639 Report.pdf
- ^ Newell, C.J., McLeod, R.K. and Gonzales, J.R., 1996. BIOSCREEN: Natural Attenuation Decision Support System - User's Manual, Version 1.3. US Environmental Protection Agency, EPA/600/R-96/087. Report.pdf BIOSCREEN website
- ^ Aziz, C.E., Newell, C.J., Gonzales, J.R., Haas, P.E., Clement, T.P. and Sun, Y., 2000. BIOCHLOR Natural Attenuation Decision Support System. User’s Manual - Version 1.0. US Environmental Protection Agency, EPA/600/R-00/008. Report.pdf BIOCHLOR website
- ^ Falta, R.W., Stacy, M.B., Ahsanuzzaman, A.N.M., Wang, M. and Earle, R.C., 2007. REMChlor Remediation Evaluation Model for Chlorinated Solvents - User’s Manual, Version 1.0. US Environmental Protection Agency. Center for Subsurface Modeling Support, Ada, OK. Report.pdf REMChlor website
- ^ Zheng, C. and Wang, P.P., 1999. MT3DMS: A Modular Three-Dimensional Multispecies Transport Model for Simulation of Advection, Dispersion, and Chemical Reactions of Contaminants in Groundwater Systems; Documentation and User’s Guide. Contract Report SERDP-99-1 U.S. Army Engineer Research and Development Center, Vicksburg, MS. Report.pdf MT3DMS website
- ^ McDonald, M.G. and Harbaugh, A.W., 1988. A Modular Three-dimensional Finite-difference Ground-water Flow Model, Techniques of Water-Resources Investigations, Book 6, Modeling Techniques. U.S. Geological Survey, 586 pages. DOI: 10.3133/twri06A1 Report.pdf Free MODFLOW download from: USGS